تسلسل فيبوناتشي: كود الطبيعة، جمال الفن، وأسرار تداول الفوركس

تسلسل فيبوناتشي هو تقدم عددي غامض متجذر بعمق ليس فقط في عالم الرياضيات بل أيضًا في الطبيعة والفن. في هذه المقالة، سنقدم لك سحره، خصائصه، ومكتشفه. سواء كنت مهتمًا بالرياضيات أم لا، ندعوك للاستمتاع بعالم فيبوناتشي المثير.

1. ما هو تسلسل فيبوناتشي؟

تسلسل فيبوناتشي هو سلسلة رقمية مثيرة للفضول رياضيًا تُبنى باستخدام خصائص الأعداد الطبيعية. مفتاح هذا التسلسل يكمن في قاعدة الجمع البسيطة. الحدّان الأولان هما “0” و”1″، وكل حدّ لاحق يُحسب دائمًا كمجموع الحدّين السابقين. في الصياغة الرياضية، يمكن التعبير عنه كما يلي:

• F(n) = F(n-1) + F(n-2) (حيث n ≥ 2)

بداية تسلسل فيبوناتشي

عند النظر عن كثب إلى تسلسل فيبوناتشي، الأعداد الأولية هي كما يلي:

• 0
• 1
• 1
• 2
• 3
• 5
• 8
• 13
• 21
• 34
• 55

كما ترى، سمة تعريفية لهذا التسلسل هي أنه يستمر إلى ما لا نهاية.

آلية الجمع الأساسية

جانب ملحوظ في تسلسل فيبوناتشي هو أن مجموع أي رقمين متجاورين ينتج الرقم التالي في التسلسل. على سبيل المثال، الرقم الثالث، “2”، هو نتيجة جمع الرقم الأول “1” والثاني “1”. وبالمثل، الرقم الرابع، “3”، يتم الحصول عليه بجمع الرقم الثاني “1” والثالث “2”. هذه الآلية الجمع البسيطة تُبرز سحر وتعمق تسلسل فيبوناتشي.

تطبيقات العالم الحقيقي لتسلسل فيبوناتشي

بعيدًا عن مجال الرياضيات، يظهر تسلسل فيبوناتشي في ظواهر حقيقية متنوعة. الخصائص والنسب المضمنة في التسلسل تُستخدم بشكل خاص في مجالات العلوم الطبيعية والاقتصاد. قد تجد حتى عناصر متأثرة بتسلسل فيبوناتشي في محيطك اليومي.

2. خصائص أعداد فيبوناتشي

تسلسل فيبوناتشي ليس مجرد سلسلة من الأعداد؛ بل يمتلك ثروة من الخصائص المثيرة. في هذا القسم، دعونا نغوص في بعض الخصائص الفريدة لتسلسل فيبوناتشي.

القابلية للكونغرامية للحدود المتجاورة

إحدى الخصائص اللافتة لتسلسل فيبوناتشي هي أن الحدود المتجاورة قابلة للكونغرامية لبعضها البعض. القابلية للكونغرامية تعني أن القاسم المشترك الأكبر بين عددين صحيحين هو 1. على سبيل المثال، عند النظر إلى الأعداد 5 و8، فهما قابلان للكونغرامية لأنه لا يوجد لهما قاسم مشترك. هذه الخاصية صالحة لجميع الحدود المتجاورة في تسلسل فيبوناتشي.

تسلسل فيبوناتشي في الطبيعة

تسلسل فيبوناتشي مشهور أيضًا بظهوره في ظواهر متنوعة في العالم الطبيعي. على وجه الخصوص في نمو النباتات، غالبًا ما تشارك أعداد فيبوناتشي في ترتيب الأوراق، وعدد الأزهار، وحتى ترتيب البذور في دوار الشمس. على سبيل المثال، عندما تُرتب بذور دوار الشمس شعاعياً من المركز إلى الخارج، غالبًا ما تستند أعدادها إلى أعداد فيبوناتشي.

الصلة بالمتوسط الذهبي

يتمتع تسلسل فيبوناتشي بعلاقة عميقة مع النسبة الذهبية. تُعتبر النسبة الذهبية، التي تقارب 1.618، رمزًا للجمال في الطبيعة والفن. في تسلسل فيبوناتشي، عند حساب النسبة بين الأعداد المتجاورة، يمكنك ملاحظة أن القيمة تتقارب تدريجيًا مع النسبة الذهبية. لهذا السبب غالبًا ما يلعب تسلسل فيبوناتشي دورًا مهمًا في التصميم والفن.

التركيب بواسطة قواعد بسيطة

يُبنى تسلسل فيبوناتشي على قاعدة بسيطة: إضافة الرقمين السابقين للحصول على الرقم التالي. يستمر التسلسل كما يلي:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

تُتيح هذه البساطة أن يمتد التسلسل إلى ما لا نهاية.

استخدام نسب فيبوناتشي

الـنسب المستخرجة من سلسلة فيبوناتشي مثيرة للاهتمام أيضًا. على وجه الخصوص في تداول الأسواق المالية، تُستخدم نسب فيبوناتشي بشكل متكرر. على وجه التحديد، هناك عدة نسب رئيسية، مثل:

• 0.236 (23.6%): التقسيم على المصطلح بعد موضعين
• 0.618 (61.8%): التقسيم على المصطلح المجاور

تُستخدم هذه النسب على نطاق واسع في تحليل الرسوم البيانية وتُعد أدوات مهمة للعديد من المستثمرين.

من الواضح أن سلسلة فيبوناتشي تسلسل رائع للغاية، إذ تمتلك جمالًا رياضيًا لا يُضاهى وتؤثر أيضًا بشكل كبير على العالم الطبيعي والثقافة.

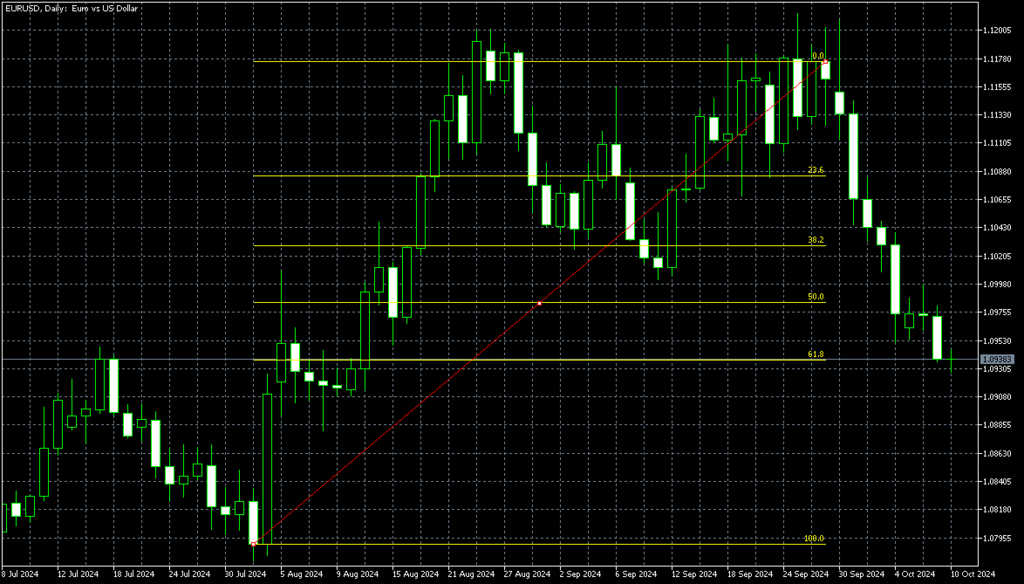
صورة: MT5 Fibonacci

3. ليوناردو فيبوناتشي، مكتشف سلسلة فيبوناتشي

حياة فيبوناتشي وخلفيته

ولد ليوناردو فيبوناتشي حوالي عام 1170 في بيزا، إيطاليا. وُهب بالموهبة الرياضية، وازدهر خلال فترة كان النشاط التجاري فيها مزدهرًا في العصور الوسطى. ساهم إنجازات فيبوناتشي ليس فقط في التجارة والرياضيات، بل أيضًا في تطوير طرق الحساب.

تأثير “ليبر أباشي”

أشهر أعمال فيبوناتشي، “ليبر أباشي” (كتاب الحساب)، نُشر في عام 1202. في هذا الكتاب، قدم وحقق شعبية سهولة الأرقام الهندية-العربية كنظام عد جديد، مبدلًا الأرقام الرومانية في ذلك الوقت. علاوة على ذلك، في هذا العمل، قدم أول مرة سلسلة فيبوناتشي من خلال مشكلة تتعلق بتكاثر الأرانب.

مشكلة الأرانب

تُعزى أصول سلسلة فيبوناتشي إلى مشكلة مبنية على طريقة تكاثر الأرانب، وال… … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … …

توجد سلسلة فيبوناتشي ليس فقط في النباتات بل أيضًا في هياكل أجسام الحيوانات. على سبيل المثال، تشعب القصبات الدموية وأوعية دم الكبد يتأثر أيضًا بأرقام فيبوناتشي. يُعتقد أن هذه الأنماط التشعبية تطورت لنقل المغذيات والأكسجين بكفاءة. في الطبيعة، الكفاءة ضرورية كجزء من استراتيجيات البقاء.

تأثير سلسلة فيبوناتشي في الفن

للسلسلة فيبوناتشي تأثير كبير على مجال الفن، حيث يجذب العديد من الفنانين نسبه الجميلة. “النسبة الذهبية” ليست منفصلة عن سلسلة فيبوناتشي وغالبًا ما تُدمج في الأعمال الفنية والتصاميم المعمارية. على سبيل المثال، يُقال إن تحفة ليوناردو دا فينشي “الموناليزا” ونسب تمثال فينوس دي ميلو مرتبطة ارتباطًا وثيقًا بسلسلة فيبوناتشي والنسبة الذهبية.

سحر الجمال الذي تخلقه سلسلة فيبوناتشي

الأشكال والنسب التي تولدها سلسلة فيبوناتشي تمتلك جمالًا فريدًا يتناغم بعمق مع الناس. يدمج العديد من الفنانين والمصممين سلسلة فيبوناتشي بنشاط لخلق تناغم بصري ومتعة جمالية. وبالتالي، يتضح أن سلسلة فيبوناتشي تلعب دورًا حيويًا ليس فقط في الظواهر الطبيعية بل أيضًا في مجال الفن.

5. كيفية استخدام سلسلة فيبوناتشي في تداول الفوركس

تُعد سلسلة فيبوناتشي أداة تحليل فني هامة جدًا في الفوركس (تداول العملات الأجنبية). على وجه الخصوص، يمكن لاستخدام تصحيح فيبوناتشي أن يساعد في توقع اتجاهات السوق ونقاط الانعكاس. هنا، سنستعرض كيفية الاستفادة من سلسلة فيبوناتشي وأمثلة عملية على استخدامها.

ما هو تصحيح فيبوناتشي؟

تصحيح فيبوناتشي هو طريقة تُستخدم لتوقع الانسحابات والارتفاعات داخل الاتجاه. تعتمد هذه التقنية على نسب فيبوناتشي المستندة إلى القمم والقيعان المتذبذبة لتحليل مقدار ما قد يتراجع فيه السعر. النسب التالية لفيبوناتشي تستحق الانتباه بشكل خاص:

• 23.6%
• 38.2%
• 50%
• 61.8%
• 100%

من خلال رسم هذه المستويات على الرسم البياني، يمكن للمتداولين الحصول على مؤشر حول الأماكن التي قد ينعكس فيها السعر.

طرق التحليل العملي باستخدام سلسلة فيبوناتشي

1. تحديد القمم والقيعان
   أولاً، حدد القمة والقيعان المتذبذبة الأخيرة داخل الرسم البياني الذي تراقبه. ارسم مستويات تصحيح فيبوناتشي بناءً على هاتين النقطتين.
2. رسم خطوط التصحيح
   باستخدام أداة مخصصة، ارسم خطوط التصحيح بناءً على القمة والقيعان المحددتين. سيظهر ذلك بوضوح مستويات السعر التي يُتوقع فيها حدوث تصحيحات أو انعكاسات.
3. تأكيد الإشارات
   عندما تتطابق خطوط التصحيح مع مؤشرات فنية أخرى (مثل المتوسطات المتحركة أو خطوط الدعم/المقاومة)، تصبح تلك الخطوط إشارة أقوى. على سبيل المثال، إذا كان خط الـ 61.8% يتماشى مع إشارات تأكيدية أخرى، يمكن استخدامه كنقطة دخول للشراء أو البيع.

أدوات تحليل فيبوناتشي الأخرى

إلى جانب التصحيح، يمكن الاستفادة من سلسلة فيبوناتشي بطرق مختلفة أخرى. إليك بعضًا منها:

• مراوح فيبوناتشي
  تتضمن هذه الطريقة رسم خطوط متشعبة من قمة وقيعان لتحديد نقاط تغير الاتجاه. يمكن أن يساعد استخدام ذلك في فهم خطوط اتجاه السوق بسهولة أكبر.
• أقواس فيبوناتشي
  تتضمن هذه الطريقة رسم أقواس لتوقع نطاق تقلبات السعر ومستويات الدعم/المقاومة المستقبلية. من خلال ملاحظة كيفية تأثير الأقواس على الأسعار، يمكنك تأكيد اتجاه الاتجاه.

العوامل النفسية وفيبوناتشي

أحد الأسباب التي تجعل سلسلة فيبوناتشي فعّالة بشكل خاص في سوق الفوركس هو سيكولوجية المتداولين. نظرًا لأن العديد من المتداولين يستخدمون تصحيح فيبوناتشي، تصبح هذه المستويات السعرية بطبيعتها مهمة وغالبًا ما تُحدث ردود فعل في السوق. لذلك، دمج فيبوناتشي في استراتيجيتك التداولية يمكن أن يمنحك ميزة من حيث التوقعات ونهجك العام.

الخلاصة

تسلسل فيبوناتشي ليس مجرد مفهوم رياضي؛ إنه فكرة مثيرة للغاية متشابكة بعمق مع الطبيعة والفن. نسبه الجميلة وخصائصه الغامضة تؤثر على حياتنا بطرق مختلفة. خصوصًا في سوق الفوركس، يُعد تحليل فيبوناتشي مؤشرًا تقنيًا حاسمًا، مما يجعله أداة مفيدة للمتداولين. تسلسل فيبوناتشي هو كيان رائع يُظهر تقاطع الرياضيات والطبيعة والمجتمع البشري.

الأسئلة المتكررة

ما هو تسلسل فيبوناتشي؟

تسلسل فيبوناتشي هو أحد أشهر السلاسل في الرياضيات. يبدأ بالرقمين الأولين 0 و1، ويُحسب كل رقم لاحق على أنه مجموع الرقمين السابقين. هذه القاعدة البسيطة تسمح للسلسلة بالاستمرار إلى ما لا نهاية. يمتلك تسلسل فيبوناتشي العديد من الخصائص المثيرة وهو سلسلة مهمة تُوجد في الطبيعة والفنون.

كيف يُستخدم تسلسل فيبوناتشي في الطبيعة والفن؟

يتداخل تسلسل فيبوناتشي بعمق مع العديد من الظواهر الطبيعية، مثل أنماط نمو النباتات، وعدد بتلات الزهور، وترتيب بذور دوار الشمس. كما يلعب دورًا مهمًا في الفنون، بما في ذلك العمارة والرسم والموسيقى، غالبًا فيما يتعلق بنسبة الذهب. النسب الجميلة التي يخلقها تسلسل فيبوناتشي هي ميزة جذابة تجذب قلوب الناس.

كيف يُستخدم تسلسل فيبوناتشي في تداول الفوركس؟

في تداول الفوركس، يُستخدم تصحيح فيبوناتشي كأحد أهم أدوات التحليل الفني. تساعد هذه الطريقة في تحديد المستويات المحددة التي قد ترتد فيها الأسعار، استنادًا إلى القمم والقيعان السابقة. تُستَخدم أيضًا طرق تحليل أخرى مثل مراوح فيبوناتشي وأقواس فيبوناتشي. العوامل النفسية للمتداولين تؤثر أيضًا على فعالية تسلسل فيبوناتشي.

أخبرني عن ليوناردو فيبوناتشي، مكتشف تسلسل فيبوناتشي.

ليوناردو فيبوناتشي كان رياضياتيًا وُلد حوالي عام 1170 في بيزا، إيطاليا. في كتابه «Liber Abaci»، لم يقتصر دوره على نشر مزايا الأرقام الهندية-العربية فحسب، بل قدم أيضًا لأول مرة تسلسل فيبوناتشي من خلال مسألة تتعلق بتكاثر الأرانب. تجاوزت إنجازات فيبوناتشي مجرد سلسلة، حيث جلبت تأثيرات مبتكرة إلى مجال الرياضيات بأكمله. لقد انتقل اسمه عبر الأجيال كرمز للرياضيات.