Dãy Fibonacci không chỉ là một khái niệm toán học, mà còn ẩn sâu trong thế giới tự nhiên và nghệ thuật. Dãy số kỳ diệu này có sức hấp dẫn và những đặc điểm riêng. Trong bài viết này, chúng tôi sẽ giới thiệu về những đặc trưng đó cũng như người đã khám phá ra nó. Dù bạn có hứng thú với toán học hay không, hãy cùng khám phá thế giới bí ẩn của dãy Fibonacci.
1. Dãy Fibonacci là gì?
Dãy Fibonacci là một chuỗi số tự nhiên có đặc điểm toán học phong phú. Điểm nổi bật của dãy số này nằm ở quy tắc cộng đơn giản. Hai số đầu tiên là “0” và “1”, các số tiếp theo được tính bằng tổng của hai số đứng trước nó. Công thức được biểu diễn như sau:
- F(n) = F(n-1) + F(n-2)(trong đó n ≥ 2)
Khởi đầu của dãy Fibonacci
Nếu xem xét kỹ hơn, dãy Fibonacci bắt đầu với các số sau:
- 0
- 1
- 1
- 2
- 3
- 5
- 8
- 13
- 21
- 34
- 55
Đặc điểm của dãy số này là nó có thể kéo dài vô tận.
Cơ chế cộng cơ bản
Điểm đáng chú ý của dãy Fibonacci là tổng của hai số liền kề sẽ tạo ra số tiếp theo. Ví dụ, số thứ ba “2” là kết quả của việc cộng số thứ nhất “1” và số thứ hai “1”. Tương tự, số thứ tư “3” được tạo ra bằng cách cộng số thứ hai “1” và số thứ ba “2”. Cơ chế cộng đơn giản này đã làm tăng thêm sức hấp dẫn và chiều sâu của dãy Fibonacci.
Ứng dụng dãy Fibonacci trong thế giới thực
Dãy Fibonacci không chỉ giới hạn trong toán học mà còn xuất hiện trong nhiều hiện tượng của thế giới thực. Đặc điểm và tỉ lệ của dãy số này được ứng dụng rộng rãi trong các lĩnh vực như khoa học tự nhiên và kinh tế học. Có thể bạn đã từng bắt gặp những thứ xung quanh mình chịu ảnh hưởng bởi dãy Fibonacci.

2. Đặc điểm của số Fibonacci
Dãy Fibonacci không chỉ là một chuỗi số thông thường mà còn chứa đựng rất nhiều đặc điểm thú vị. Trong phần này, chúng ta sẽ cùng khám phá một số đặc trưng độc đáo của dãy Fibonacci.
Tính nguyên tố cùng nhau của các số liền kề
Một trong những đặc điểm nổi bật của dãy Fibonacci là các số liền kề nguyên tố cùng nhau. Nguyên tố cùng nhau có nghĩa là ước số chung lớn nhất của hai số nguyên bằng 1. Ví dụ, xem xét số 5 và 8, chúng không có ước số chung nào ngoại trừ 1 nên chúng nguyên tố cùng nhau. Đặc tính này áp dụng cho tất cả các cặp số liền kề trong dãy Fibonacci.
Dãy Fibonacci trong tự nhiên
Dãy Fibonacci còn được biết đến với việc xuất hiện trong nhiều hiện tượng tự nhiên. Đặc biệt là trong sự phát triển của thực vật, số lượng cánh hoa, cách sắp xếp lá trên thân cây, hay thậm chí cách sắp xếp hạt hướng dương thường liên quan đến các số Fibonacci. Chẳng hạn, khi các hạt hướng dương được sắp xếp theo hình xoắn ốc từ trung tâm ra ngoài, số lượng của chúng thường dựa trên các số Fibonacci.
Mối liên hệ với tỷ lệ vàng
Dãy Fibonacci có mối liên hệ sâu sắc với tỷ lệ vàng. Tỷ lệ vàng xấp xỉ 1.618 và được coi là biểu tượng của vẻ đẹp trong tự nhiên và nghệ thuật. Khi tính tỷ lệ của các số liền kề trong dãy Fibonacci, bạn sẽ thấy giá trị này dần dần tiến đến tỷ lệ vàng. Do đó, dãy Fibonacci thường đóng vai trò quan trọng trong thiết kế và nghệ thuật.
Cấu tạo dựa trên quy tắc đơn giản
Dãy Fibonacci được xây dựng dựa trên một quy tắc đơn giản: cộng hai số đứng trước nó để tạo ra số tiếp theo. Dãy số này tiếp tục như sau:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Sự đơn giản này cho phép dãy số có thể kéo dài vô tận.
Ứng dụng tỷ lệ Fibonacci
Tỷ lệ được rút ra từ dãy Fibonacci cũng rất thú vị. Đặc biệt, trong giao dịch thị trường tài chính, tỷ lệ Fibonacci thường được sử dụng. Cụ thể, có những tỷ lệ quan trọng sau:
- 0.236 (23.6%): Lấy số hạng sau chia cho số hạng cách nó 2 vị trí
- 0.618 (61.8%): Lấy số hạng sau chia cho số hạng liền kề
Những tỷ lệ này được sử dụng rộng rãi trong phân tích biểu đồ và là công cụ quan trọng đối với nhiều nhà đầu tư.
Nhờ những đặc điểm trên, dãy Fibonacci không chỉ mang vẻ đẹp toán học mà còn có ảnh hưởng lớn đến thế giới tự nhiên và văn hóa, trở thành một dãy số vô cùng hấp dẫn.
3. Người phát hiện ra dãy Fibonacci: Leonardo Fibonacci
Cuộc đời và bối cảnh của Fibonacci
Leonardo Fibonacci (Leonardo Fibonacci) sinh ra tại Pisa, Ý, vào khoảng năm 1170. Ông là một nhà toán học tài năng, hoạt động trong thời kỳ mà hoạt động thương mại đang phát triển mạnh mẽ. Những đóng góp của Fibonacci không chỉ ảnh hưởng đến thương mại và toán học mà còn cả sự phát triển của các phương pháp tính toán.
Ảnh hưởng của cuốn “Liber Abaci”
Cuốn sách nổi tiếng nhất của Fibonacci, “Liber Abaci” (Cuốn sách về tính toán), được xuất bản vào năm 1202. Trong cuốn sách này, ông đã giới thiệu các chữ số Ấn Độ-Ả Rập như một phương pháp ghi số mới thay thế cho chữ số La Mã và phổ biến sự tiện lợi của chúng. Ông cũng lần đầu tiên giới thiệu dãy Fibonacci thông qua một bài toán về sự sinh sản của thỏ.
Bài toán về thỏ
Nguồn gốc của dãy Fibonacci bắt nguồn từ một bài toán về sự sinh sản của thỏ. Ông đã đặt ra một tình huống giả định về cách một cặp thỏ sinh sản và số lượng thỏ tăng lên như thế nào theo một điều kiện cụ thể. Mô hình đơn giản này đã tạo ra một chuỗi số được tạo thành bằng cách cộng hai số đứng trước nó.
Tính sáng tạo trong các công trình của Fibonacci
Một trong những thành tựu lớn nhất của Fibonacci là mang đến những ý tưởng đột phá cho lĩnh vực toán học ở châu Âu lúc bấy giờ. Ông không chỉ phát triển các dãy số mà còn cải tiến đáng kể các phương pháp tính toán và tư duy toán học, có ảnh hưởng to lớn đến sự phát triển của toán học sau này. Khám phá của ông không chỉ dừng lại ở một dãy số mà còn liên kết sâu sắc với tự nhiên và hình học.
Những giai thoại về Fibonacci
Trong các công trình của mình, Fibonacci thường tìm thấy những mô hình độc đáo, đôi khi được gọi là “phép màu của các con số”, đã gây ấn tượng mạnh mẽ với nhiều người. Nhờ đó, tên của ông đã trở thành biểu tượng của toán học qua nhiều thế hệ và vẫn có ảnh hưởng đến giáo dục toán học hiện đại.
Tính phổ quát của các con số
Dãy số mà ông khám phá không chỉ mang tính toán học mà còn là chìa khóa để tìm thấy vẻ đẹp và sự hài hòa trong nhiều lĩnh vực khác nhau như tự nhiên, nghệ thuật và kiến trúc. Tên của Fibonacci không chỉ tượng trưng cho dãy số mà còn tượng trưng cho tư tưởng và sự tìm tòi toán học của ông, và nó tiếp tục lan truyền rộng rãi.
4. Dãy Fibonacci trong tự nhiên và nghệ thuật
Dãy Fibonacci xuất hiện trong tự nhiên
Sự hiện diện của dãy Fibonacci trong tự nhiên thật sự rất hấp dẫn. Dãy số này nổi bật trong sự phát triển của thực vật. Ví dụ, số cánh hoa của nhiều loài hoa thường trùng với các số Fibonacci như “3”, “5”, “8”. Đặc biệt, ở các loài thực vật họ cúc, các số như 13 và 21 xuất hiện rất thường xuyên.
Dãy Fibonacci cũng được quan sát thấy trong cách sắp xếp hạt hướng dương. Hướng dương sắp xếp hạt theo hình xoắn ốc theo chiều kim đồng hồ và ngược chiều kim đồng hồ, và số lượng các xoắn ốc này dựa trên các số Fibonacci. Cách sắp xếp này là một ví dụ điển hình về việc thực vật tận dụng không gian một cách tối đa.
Vai trò của dãy Fibonacci trong thế giới động vật
Dãy Fibonacci không chỉ xuất hiện ở thực vật mà còn trong cấu trúc cơ thể động vật. Ví dụ, sự phân nhánh của phế quản và mạch máu gan cũng chịu ảnh hưởng của các số Fibonacci. Những nhánh này được cho là đã phát triển trong quá trình tiến hóa để vận chuyển chất dinh dưỡng và oxy một cách hiệu quả. Trong tự nhiên, hiệu quả là một phần rất quan trọng của chiến lược sinh tồn.
Ảnh hưởng của dãy Fibonacci trong nghệ thuật
Dãy Fibonacci cũng có ảnh hưởng quan trọng trong lĩnh vực nghệ thuật, nhiều nghệ sĩ bị hấp dẫn bởi những tỷ lệ đẹp của nó. “Tỷ lệ vàng” có liên quan mật thiết đến dãy Fibonacci và thường được sử dụng trong các tác phẩm nghệ thuật và thiết kế kiến trúc. Ví dụ, kiệt tác “Mona Lisa” của Leonardo da Vinci và tỷ lệ của bức tượng Vệ Nữ thành Milo được cho là có liên quan đến dãy Fibonacci và tỷ lệ vàng.
Vẻ đẹp hấp dẫn của dãy Fibonacci
Các hình dạng và tỷ lệ do dãy Fibonacci tạo ra mang một vẻ đẹp độc đáo, là yếu tố sâu sắc lay động lòng người. Nhiều nghệ sĩ và nhà thiết kế chủ động sử dụng dãy Fibonacci để tạo ra sự hài hòa và dễ chịu về mặt thị giác. Có thể thấy, dãy Fibonacci đóng vai trò quan trọng không chỉ trong các hiện tượng tự nhiên mà còn cả trong lĩnh vực nghệ thuật.

5. Cách sử dụng dãy Fibonacci trong FX
Dãy Fibonacci là một trong những công cụ phân tích kỹ thuật rất quan trọng trong FX (Giao dịch ngoại hối). Đặc biệt, việc sử dụng Fibonacci Retracement có thể giúp dự đoán xu hướng và các điểm đảo chiều của thị trường. Dưới đây, chúng ta sẽ cùng tìm hiểu chi tiết về cách sử dụng dãy Fibonacci và ví dụ thực tế.
Fibonacci Retracement là gì?
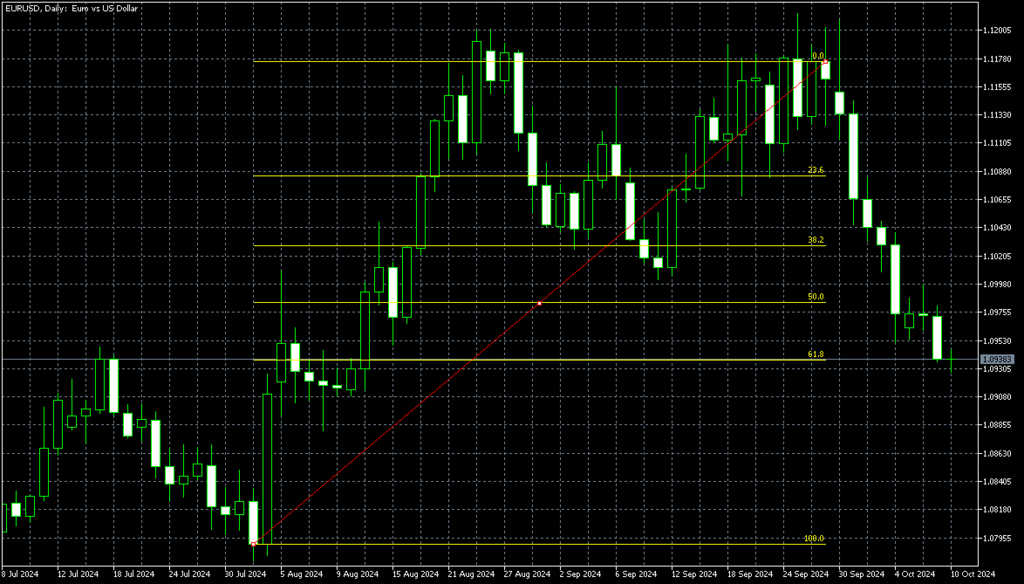
Fibonacci Retracement là một phương pháp dùng để dự đoán các điểm thoái lui hoặc đảo chiều của một xu hướng. Phương pháp này sử dụng các tỷ lệ Fibonacci dựa trên mức giá cao nhất và thấp nhất để phân tích mức độ hồi phục của giá. Các tỷ lệ Fibonacci đáng chú ý sau đây:
- 23.6%
- 38.2%
- 50%
- 61.8%
- 100%
Bằng cách vẽ các đường này trên biểu đồ, các nhà giao dịch có thể xác định các mức giá mà tại đó giá có thể đảo chiều.
Phương pháp phân tích thực tế bằng cách sử dụng dãy Fibonacci
Xác định mức giá cao nhất và thấp nhất
Trước tiên, hãy xác định mức giá cao nhất và thấp nhất gần đây trên biểu đồ bạn đang quan sát. Sau đó, vẽ Fibonacci Retracement dựa trên hai điểm này.Vẽ các đường Retracement
Sử dụng công cụ chuyên dụng để vẽ các đường Retracement dựa trên mức giá cao nhất và thấp nhất đã xác định. Điều này sẽ làm rõ các mức giá mà tại đó có thể xảy ra sự đảo chiều hoặc hồi phục.Xác nhận tín hiệu
Khi các đường Retracement trùng với các chỉ báo kỹ thuật khác (như đường trung bình động hoặc các đường hỗ trợ/kháng cự), tín hiệu đó càng trở nên mạnh mẽ hơn. Ví dụ, nếu đường 61.8% trùng khớp với các tín hiệu xác nhận khác, nó có thể được sử dụng làm điểm vào lệnh mua hoặc bán.
Các công cụ phân tích Fibonacci khác
Ngoài Retracement, dãy Fibonacci còn có thể được áp dụng theo nhiều cách khác nhau. Dưới đây là một vài ví dụ:
Fibonacci Fan
Đây là phương pháp vẽ các đường tỏa ra từ mức giá cao nhất và thấp nhất để tìm điểm thay đổi xu hướng. Sử dụng công cụ này giúp bạn dễ dàng nắm bắt được đường xu hướng của thị trường.Fibonacci Arc
Đây là phương pháp vẽ các đường cung để dự đoán phạm vi biến động giá hoặc các mức hỗ trợ/kháng cự tiếp theo. Quan sát cách các đường cung ảnh hưởng đến giá có thể giúp bạn xác nhận hướng của xu hướng.
Yếu tố tâm lý và Fibonacci
Một trong những lý do khiến dãy Fibonacci đặc biệt hiệu quả trong thị trường FX là vì yếu tố tâm lý của các nhà giao dịch. Vì nhiều nhà giao dịch sử dụng Fibonacci Retracement, các mức giá này tự nhiên trở nên quan trọng và thường gây ra phản ứng của thị trường. Do đó, giao dịch dựa trên Fibonacci có thể mang lại lợi thế trong việc dự đoán và xây dựng chiến lược của bạn.

Tóm tắt
Dãy Fibonacci không chỉ là một khái niệm toán học đơn thuần, mà còn là một khái niệm rất thú vị liên quan sâu sắc đến thế giới tự nhiên và nghệ thuật. Tỷ lệ đẹp và các đặc tính kỳ diệu của nó đã ảnh hưởng đến cuộc sống của chúng ta theo nhiều cách khác nhau. Đặc biệt trong thị trường FX, phân tích Fibonacci đã trở thành một trong những chỉ báo kỹ thuật quan trọng và là công cụ hữu ích cho các nhà giao dịch. Dãy Fibonacci là một sự tồn tại tuyệt vời, thể hiện sự giao thoa giữa toán học, tự nhiên và xã hội loài người.
Câu hỏi thường gặp
Dãy Fibonacci là gì?
Dãy Fibonacci là một trong những dãy số nổi tiếng nhất. Nó bắt đầu với hai số đầu tiên là 0 và 1, và các số tiếp theo được tính bằng tổng của hai số đứng trước. Với quy tắc đơn giản này, dãy số có thể kéo dài vô tận. Dãy Fibonacci có nhiều đặc điểm thú vị và là một dãy số quan trọng được tìm thấy trong tự nhiên và nghệ thuật.
Dãy Fibonacci được sử dụng trong tự nhiên và nghệ thuật như thế nào?
Dãy Fibonacci có liên quan sâu sắc đến nhiều hiện tượng tự nhiên như mô hình phát triển của thực vật, số cánh hoa, và cách sắp xếp hạt hướng dương. Dãy số này cũng đóng vai trò quan trọng trong nghệ thuật, kiến trúc và âm nhạc, liên quan đến tỷ lệ vàng. Tỷ lệ đẹp mà dãy Fibonacci tạo ra là một đặc điểm hấp dẫn, thu hút sự chú ý của con người.
Dãy Fibonacci được sử dụng trong FX như thế nào?
Trong FX, Fibonacci Retracement được sử dụng như một công cụ phân tích kỹ thuật quan trọng. Phương pháp này dựa trên các mức giá cao nhất và thấp nhất trong quá khứ để tìm ra các mức giá tiềm năng có thể đảo chiều. Ngoài ra, các phương pháp phân tích khác như Fibonacci Fan và Fibonacci Arc cũng được sử dụng. Yếu tố tâm lý của các nhà giao dịch cũng ảnh hưởng đến tính hiệu quả của dãy Fibonacci.
Bạn có thể cho tôi biết về Leonardo Fibonacci, người đã phát hiện ra dãy số này không?
Leonardo Fibonacci là một nhà toán học sinh ra tại Pisa, Ý, vào khoảng năm 1170. Trong cuốn sách “Liber Abaci” của mình, ông đã phổ biến những ưu điểm của chữ số Ấn Độ-Ả Rập và lần đầu tiên giới thiệu dãy Fibonacci thông qua một bài toán về sự sinh sản của thỏ. Những thành tựu của Fibonacci không chỉ dừng lại ở một dãy số mà còn có ảnh hưởng đột phá đến toàn bộ lĩnh vực toán học. Tên của ông đã trở thành biểu tượng của toán học qua nhiều thế hệ.











